Because of the restrictions of a computer interface, there are some special points you will need to understand to enter all functions.
Special Symbols
Because mathematicians use many symbols not normally found on a computer keyboard, the graph tool uses a small number of special symbols, codes and abbreviations in order to allow you to enter functions.
Normal Symbol |
Graph Tool |
Notes |
|
Multiplication |
´ |
* |
|
Exponentiation (Powers) |
none (eg 2x) |
^ (eg 2^x) |
Only needed when the graph tool fails to automatically recognise the power. |
Division |
÷ |
/ (followed by a space) |
The / character is more often used (without the space) to enter fractions. |
Pi |
π |
pi |
Can be used in both functions and axes. |
Theta |
θ |
th |
Used in polar functions |
Greater than or equal to |
≥ |
>= |
|
Less than or equal to |
≤ |
<= |
|
Plus Minus |
± |
+- |
the graph tool will automatically graph both arms of the function. |
Most of these symbols are in common use in computer based mathematics.
Brackets
Many functions, especially fractions, contain assumed brackets. The graph tool will sometimes require you to enter these brackets even though you cannot see them. For example, if you enter y = 3/x+3 does this mean
![]()
To graph the second function you need to add logical brackets to your function and type y = 3/(x+3). These brackets will not be displayed but will influence how your function is interpreted.
As a general rule, if the function is not shown formatted correctly by the graph tool, add some brackets to make your meaning clear.
A very important use of brackets is to logically identify the numerator and denominator in complicated fractions. For example: (x+2)/(x-3) needs the brackets to be interpreted as ![]() rather than
rather than ![]() .
.
Brackets are also used to logically identify powers and ensure that the graph tool interprets your function correctly.
All three bracket types {, [ and ( may be used interchangeably in the graph tool and the graph tool makes no distinction between them. the graph tool does not even check to see if brackets are paired. You are responsible for this. If there is a fraction inside a bracket, the bracket is automatically resized.
Example:
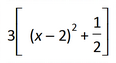 is entered as 3[(x-2)2+1/2]
is entered as 3[(x-2)2+1/2]
Powers
Most powers will be automatically recognized by the graph tool. The graph tool will not automatically recognize powers if
| • | you require a variable as a power |
| • | you require a function as a power |
| • | you require a power of a number |
| • | you require a complicated power. |
In these cases you need to explicitly indicate the power using the ^ symbol. As with fractions, complicated powers need to be surrounded with brackets. These brackets will not be displayed.
Examples:
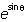 is entered as e^(sinth)
is entered as e^(sinth)
![]() is entered as x^(2y+3)
is entered as x^(2y+3)
Spaces
Spaces change the way a particular equation is formatted and therefore interpreted. This can best be illustrated using these examples.
![]() is entered as sin2 th
is entered as sin2 th
![]() is entered as sin 2th
is entered as sin 2th
The only difference between the two equations is the location of a space.